Тази година под контрола на Свилен Искров отново бях автор на задачите за ежегодното състезание по физика на Фондация Миньо Балкански.
Както писах след конкурса от 2011:
Ако не сте млад физик или физичка вероятно не сте чували за него (Всъщност има и конкурс по математика). Но ако сте от моята каста то знаете за претенциите, че конкурсът е на същото високо ниво като националната олимпиада (обикновено тези претенции са напълно обосновани). И както националната олимпиада е пътят за участие в отбора за IPhO, така и конкурсът по физика на фондация Миню Балкански отваря вратите за обучение във френско висше училище (знаехте това… нали?). Но тук ще говоря за задачите които аз дадох и за работите които аз проверих. За детайли относно конкурса погледнете сайта на фондацията.
Задачите (които можете да свалите тук)
Горния линк дава версия с отговорите.
Дадени бяха 3 задачи за 4-ри часа на теми, съответно, еластичност на твърди тела, термодинамика на звездите и една задача проверяваща дали участниците знаят какво е потенциална енергия. Точките за всяка задача бяха съответно 19, 17 и 9.
Първа задача - Греди и еластичност.
Следните три картинки описват цялата задача:
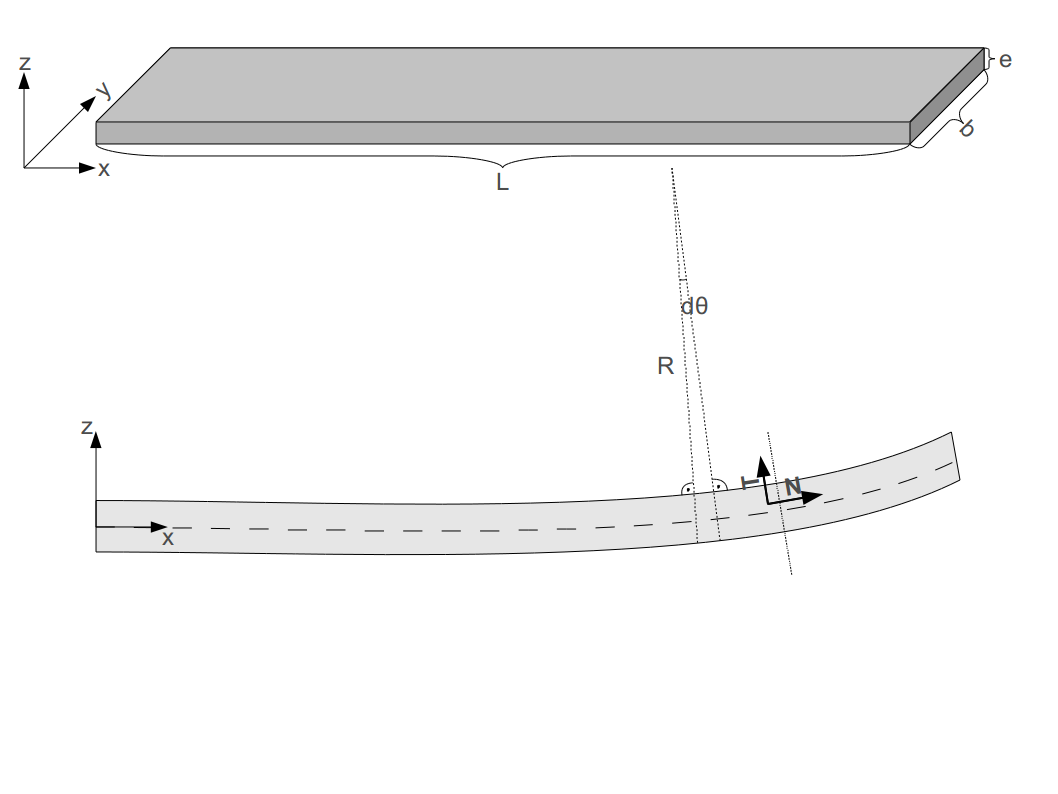
Тънка плоска греда, която ще се огъва само в една равнина.
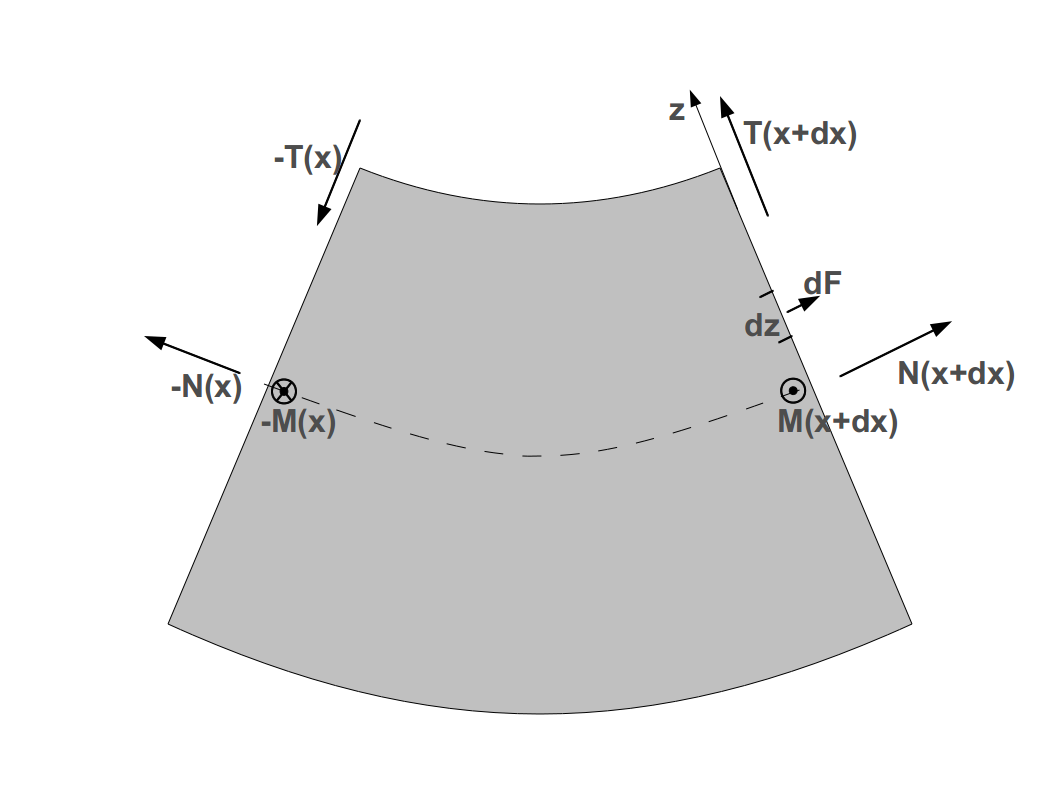
За да намерим как ще се огъва при различни натоварвания ще разледаме силите и въртящите моменти върху всяко сечение на гредата.
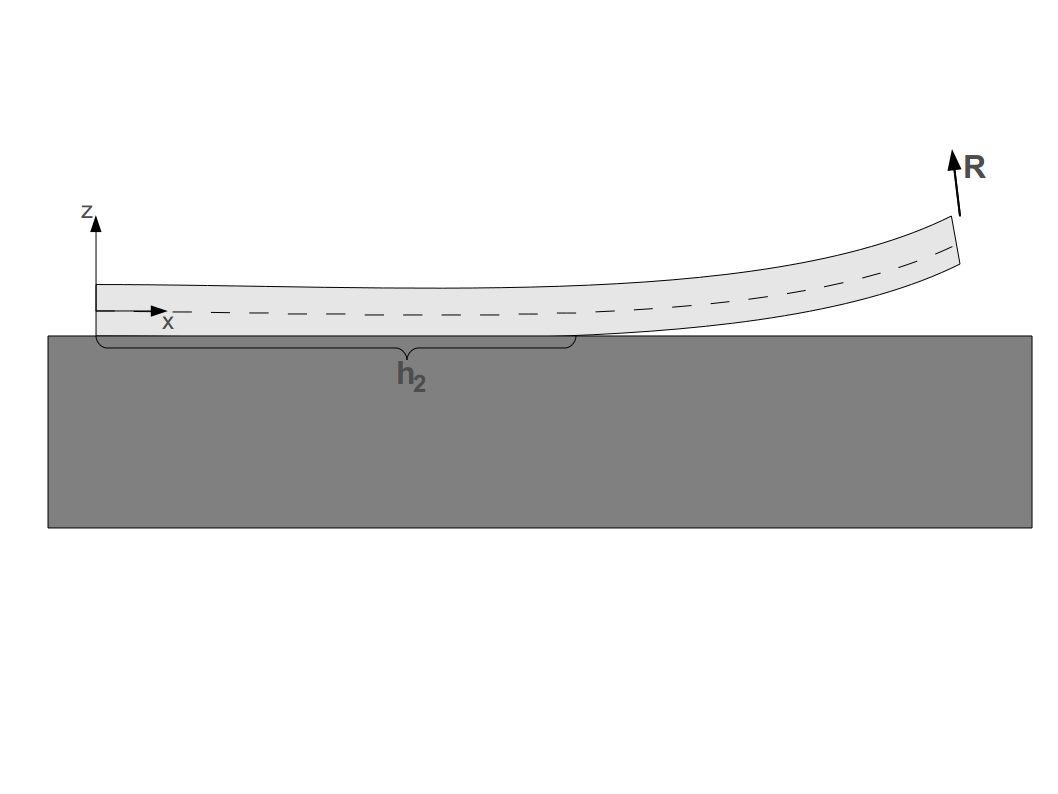
И ще приложим наученото в няколко примера, в които прилагаме напречна сила в края на гредата.
Първото приложение е да изучим как реагират миниатюрните сонди използван в атомните микроскопи. Сондата е под формата на мини-греда огъвана от привличането на атомите които заснема. Силата с която атомът привлича сондата показва какво е разстоянието между тях.
Вторият пример разглеждаше равновесието между две потенциални енергии - тази породена от залепването на две повърхности и тази породена от огъването при опитите за отлепяне на гредата от дадената повърхност.
Коментари
Само 5 от 18-те участника са погледнали задачата и никой не се е опитал да направи нещо повече от началните сметки (т.е. никой не е погледнал двете подзадачи за приложения, което много ме натъжава, защото особено втората подзадача съдържаше доста симпатични трикове за смятане на равновесно положение).
Много от участниците не са били съвсем наясно как да сметнат въртящия момент на сила разпределена по сечението на гредата. За онагледяване да вземем следния пример:
# сегмент (сечение от гредата)
# /
# ###--------->
# # #------->
# # #----->
# # #--->
# # #->
# #X#
# <-# #
# <---# #
# <-----# #
# <-------# #
# <---------###
# \
# сили действащи по повърхността на сегмента
Каква е общата сила действаща на сегмента? Силата е нула защото за всеки елемент притиснат в едната посока има елемент притиснат в обратната. Някои са сметнали силата грешно, защото са сумирали абсолютната стойност на силата, без да вземат предвид посоката.
А колко е въртящия момент? Някои, които правилно са сметнали силата (= нула), твърдят че въртящия момент също е нула, защото сляпо са казали \(M_{въртящ\ момент} = L\times F\) където \(F=0\) и \(L\) е някаква дължина. Това е грешно, защото силата приложена на всеки елемент има различно рамо и причинява различен въртящ момент. Сумата на всички елементарни въртящи моменти не е нула (както може да се види от картинката).
Резултати
Таблицата показва за всеки дял от задачата, кой колко точки е получил, заедно с максималния брой точки.
| Участник | 1.1.1 | 1.1.2 | 1.1.3 | 1.1.4 | 1.1.5 | 1.1.6 | 1.1.7 | 1.1.8 | 1.2.1 | 1.2.2 | 1.2.3 | общо |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| максимум | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 19 |
| 1 | 1 | 1 | 1 | 1 | 0.5 | 4.5 | ||||||
| 2 | ||||||||||||
| 3 | 0.75 | 0.75 | ||||||||||
| 4 | 1 | 1 | 1 | 0.5 | 1 | 4.5 | ||||||
| 5 | ||||||||||||
| 6 | 1 | 1 | 1 | 3 | ||||||||
| 7 | 1 | 1 | ||||||||||
| 8 | ||||||||||||
| 9 | ||||||||||||
| 10 | ||||||||||||
| 11 | ||||||||||||
| 12 | ||||||||||||
| 13 | ||||||||||||
| 14 | ||||||||||||
| 15 | ||||||||||||
| 16 | ||||||||||||
| 17 | ||||||||||||
| 18 |
Втора задача - Как така звездите са стабилни?
Цялата задача се въртеше около странния факт че звездите изстиват при добавяне на енергия. Ако не беше този факт (породен от гравитационните сили имащи “дълъг” обхват) то звездите щяха да са нестабилни, защото малко увеличение на температурата причинява по-бързи ядрени реакции, които от своя страна отделят повече енергия, която наивно бихме очаквали да повиши температурата още повече и т.н. докато не се случи нещо много лошо.
Коментари
11 от 18-те участника са погледнали втора задача, но никой не е успял да обясни защо звездите са стабилни. Като автор, аз съм ги затруднил ненужно на едно място (неволно). Към края на задачата, не съм споменал че дадена температура може да се вземе като константа и не зависи от радиуса на звездата.
Имаше две много често повтаряни грешки още в началото на задачата:
- смятането на потенциалната енергия: Много участници са запаметили без да разбиране следната формула: \(F = grad(E)\). Даже да пренебрегнем грешките от тип “това вектор ли е… сигурно няма значение”, “плюс или минус да сложа тук” и т.н. пак има големи проблеми с тази формула. Преди всичко - формулата е безмислена в нашия случай. Не говорим за частица движеща се в някакво потенциално поле, а за хомогенно тяло и потенциалната енергия на взаимодействията на различни части от тялото. Много от участниците просто са търсели как да напишат нещо приличащо на интеграл без оглед какви променливи всъщност интегрират. Някои състезатели са се опитали да сметнат приблизителни резултати, което не е лошо, но в случая има точно решение. Други са решили да разгледат тялото като голям брой точкови маси и да търсят средната енергия на двойка частици, но това е лоша идея, имайки предвид че е неточно и че в условието не се говори за частици.
- смятането на времето на падане: Някои са се опитали да смятат елиптични интеграли (някои от интегралите грешни поради предищни грешки), други са търсели приблизителни решения. В случая законът на Кеплер дава точно решение на два реда. И е интересно да се видят числените резултати: 30 минути за колапс на слънцето и няколко милиона години за междугалактически облак.
Други по-рядко срещани грешки са:
- при намирането на скоростта на звука в газа по метода на размерносттите, някои участници са решили ще скоростта трябва да зависи от някои странни параметри (размера на облака примерно)
- при разглеждането на звездата като идеален газ някои участници не са съвсем наясно какво влиза в уравнението за идеалния газ \(pV=\nu R_gT\). Примерно, някои взимат за обем целия обем на звездата, а за налягане, локалното налягане за дълбочината която разглеждат.
Резултати
| Участник | 2.1.1 | 2.1.2 | 2.1.3 | 2.2 | общо |
|---|---|---|---|---|---|
| максимум | 4 | 2 | 2 | 9 | 17 |
| 1 | 2.5 | 0.5 | 1 | 4 | |
| 2 | 1.75 | 2 | 1 | 1.5 | 6.25 |
| 3 | 1.5 | 1.25 | 1 | 3.75 | |
| 4 | 0.25 | 0.25 | |||
| 5 | 0.25 | 0.25 | |||
| 6 | |||||
| 7 | 0.25 | 0.25 | 0.25 | 0.75 | |
| 8 | 0.25 | 1 | 0.75 | 2 | |
| 9 | 1 | 1 | |||
| 10 | |||||
| 11 | 0.25 | 0.25 | |||
| 12 | 0.25 | 0.25 | |||
| 13 | |||||
| 14 | 0.25 | 0.25 | |||
| 15 | |||||
| 16 | |||||
| 17 | |||||
| 18 |
Трета задача - Равновесие, потенциална енергия и локални минимуми
За трета задача беше необходимо само едно нещо. Да се знае че дадена система може да има няколко стабилни равновесни положения (локални минимуми на потенциалната енергия). Тази дреболия води до невероятно голямо разнообразие от проблеми и води до невероятно красива и абстрактна математика.
Преди всичко - за да минем от едно равновесно положение в друго, обикновено трябва да минем през състояние с висока потенциална енергия. Всъщност, точно тази потенциална бариера е нещото което ни държи в равновеси в началото. Проблемът се появява когато искаме да намерим състоянието с най-ниска потенциална енергия, т.е. състоянието от което най-трудно се отива в други равновесни състояния. Когато някой протеин в тялото не успее да го направи, се появява смъртоносно прионно заболяване, примерно луда крава. Когато някой инженер не успее да го направи, нестабилност в строежа може да бъде създадена.
Интересното (с невероятни и сложни последствия) е че да се намери локален минимум е лесно, но намирането на глобалния минимум е невероятно трудно.
Коментари
14 от 18-те участника са погледнали задачата и някои даже са отговорили на по-интересните въпроси.
Никой не се е сетил че вертикални пръчици между две равнини може да се ползва за решаване на лесни Щайнерови дървета (сапунената ципа между пръчиците ще минимизира разстоянията).
Повечето участници са схванали какво е потенциалната енергия и как тя определя еволюцията на една система. Има няколко графики които са приемливи като онагледяване на въпроса за динамита, но само една графика е безгрешна (има още няколко които са получили пълния брой точки за въпроса):
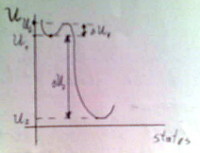
Но в някои от работите има и сериозни грешки. Като твърдението че висока потенциална енергия води до стабилност (грешката вероятно идва от объркване относно знаците пред резлични формули за потенциалната енергия). Напротив, високата потенциална енергия означава “скоро ще се разпадне”. Нещо на върха на планина, готово да се търкули долу е с висока потенциална енергия. Нещо ниско в долината, което не може да се измъкне, е с ниска потенциална енергия. Същото важи за молекули и атомни връзки: TNT има висока потенциална енергия (почти нестабилни връзки) в сравнение с много стабилните връзки на въглереодния диоксид.
Резултати
| Участник | 3.1.1.1 | 3.1.1.2 | 3.1.2 | 3.2 | общо |
|---|---|---|---|---|---|
| максимум | 2 | 2 | 4 | 1 | 9 |
| 1 | 1 | 2 | 2 | 5 | |
| 2 | 2 | 2 | 2 | 0.25 | 6.25 |
| 3 | 0.25 | 2 | 2 | 1 | 5.25 |
| 4 | 1.75 | 1.75 | |||
| 5 | 2 | 2 | 2 | 6 | |
| 6 | 0.25 | 0.25 | |||
| 7 | 0.5 | 0.25 | 0.25 | 1 | |
| 8 | |||||
| 9 | 0.25 | 0.25 | |||
| 10 | 0.25 | 0.5 | 0.75 | ||
| 11 | 0.25 | 0.25 | 0.5 | ||
| 12 | 0.25 | 0.25 | |||
| 13 | 0.25 | 0.25 | |||
| 14 | |||||
| 15 | 0.25 | 0.25 | |||
| 16 | 0.25 | 0.25 | |||
| 17 | |||||
| 18 |
Крайно класиране и резултати
Като изключим няколко дребни коментара направени за трета задача, които ме зарадваха, никой от участниците не е стигнал до най-интересните части от задачите. Повечето от писането е било по сметкаджийските части.
;( тъжен Стефо ):
Сигурен съм че би им било много забавно да разгледат по-оригиналните части от задачите, до които не са имали шанс да стигнат по време на състезанието. Всички (не само състезателите) се чуствайте свободни да обсъдите задачите и да задавате въпроси по-долу в коментарите.
Нещо интересно, което често се случва, и ще е добре състезателите да научат, е че отново високо класираните работи са сравнително лаконични. Обикновено авторите на задачите и проверяващите търсят къси отговори, не защото ги мързи да проверяват, а защото един къс отговор ясно показва дали състезателя разбира проблема, докато дългите отговори често се отклоняват в неща които нямат общо с въпроса. Разбира се, не трябва да се отива в другата крайност - лист пълен с формули и букви, но нито дума обясняваща коя буква какво означава. За жалост няколко от участниците са направили точно това.
Резултатите дадени тук са с прецизност от около +/- 0.5 точки, защото на места са давани половинчати отговори които е трудно да се оценят обективно. Това не променя реда на първенците.
| Участник | I | II | III | общо |
|---|---|---|---|---|
| максимум | 19 | 17 | 9 | 45 |
| 1 | 4.5 | 4 | 5 | 13.5 |
| 2 | 6.25 | 6.25 | 12.5 | |
| 3 | 0.75 | 3.75 | 5.25 | 9.75 |
| 4 | 4.5 | 0.25 | 1.75 | 6.5 |
| 5 | 0.25 | 6 | 6.25 | |
| 6 | 3 | 0.25 | 3.25 | |
| 7 | 1 | 0.75 | 1 | 2.75 |
| 8 | 2 | 2 | ||
| 9 | 1 | 0.25 | 1.25 | |
| 10 | 0.75 | 0.75 | ||
| 11 | 0.25 | 0.5 | 0.75 | |
| 12 | 0.25 | 0.25 | 0.5 | |
| 13 | 0.25 | 0.25 | ||
| 14 | 0.25 | 0.25 | ||
| 15 | 0.25 | 0.25 | ||
| 16 | 0.25 | 0.25 | ||
| 17 | ||||
| 18 |


Бисери
Този раздел не е написан, за да се присмиваме на участниците. Имаше няколко оригинални шеги, които ще е жалко ако само аз ги прочета. По-важно, имаше няколко грешки от които всички можем да научим нещо.
За жалост бисерите бяха доста по-малко от колкото през 2011 (вместо забавни бисери имаше гореупоменатите стандартни грешки). Ако на някого му е неприятно, че е цитиран тук, може да ми прати email и ще премахна споменаването му.
Наградата за най-голям бисер печели “####ов, баце от Враца сме!” върху почти празна работа. Засмя ме имайки предвид, че тази година проверяващия не е от Враца. Жалко, че нямаше състезатели от Бургас.
Една от работите онагледи въпроса за динамита по следния (верен, но непълен) начин:

Следва \(stuff + stuff\times dx + stuff\times (dx)^2\) - някои от състезателите се опитват да жонглират с диференциали без напълно да са разбрали какво те представляват. Вярно е че често можем да си позволим да мислим за диференциала като за “много малко парче от нещо”, но в момента в който имаме сума от диференциали с различни степени, можем да сме сигурно че сме сбъркали сериозно.
Няколко от участниците твърдят, че скоростта на звука в облак от газ трябва да зависи от големината на облака (директно). Това е неправдоподобно предположение и го маркирах като грешно. Интересното е, че даже да се приеме, след като се направи анализа на размерностите излиза, че дори да искаме \(R\) да е част от израза, не можем да го получим. За единия участник, който прави това доказателство, дадох пълния брой точки.
Това май е всичко. Поздрави на първенците! И не се притеснявайте да задавате въпроси по задачите в секцията за коментари!
